Xlam: orthotrophy and modelling failures
Wooden buildings: when and why do they rot? (Part 3)
20 June 2016
Modelling and optimization of timber structures
21 August 2016The mechanical response of timber changes in a significant way depending on the three directions characterising the material, and this is the reason why it is considered orthotropic. As it is widely known, the major strength is in the same direction of the grain, therefore structural timber elements are mostly exploited in that direction.
The Xlam production process consists in gluing massive wooden boards in crossed layers, therefore the direction of grain rotates 90 degrees for every layer. Can this material be considered orthotropic? And what happens when it is mistakenly laid 90 degrees rotated from what was expected by the project?
In the present paper we will try to answer these questions by analysing a statically and geometrically determined model, in which only the mechanical properties and the orientation of the material will be modified.
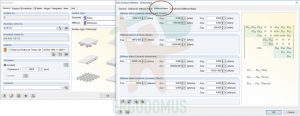
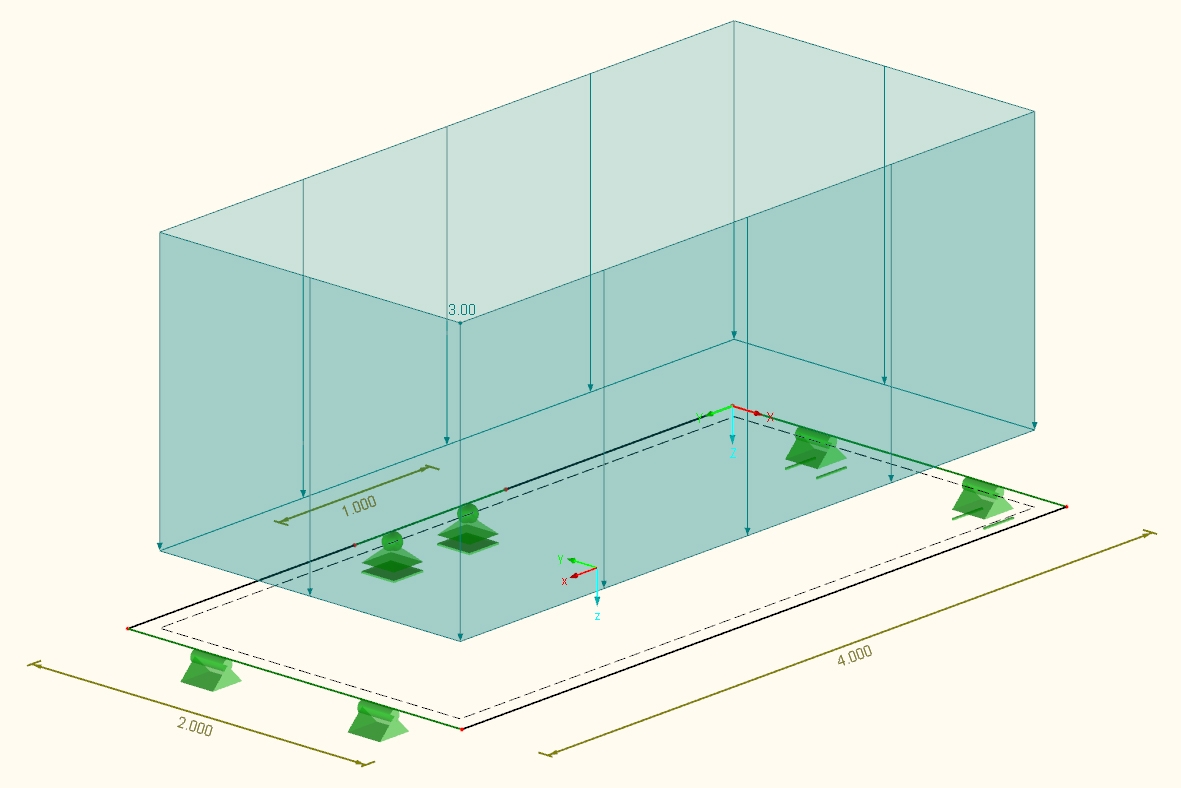
By means of the finite elements software Dlubal RFEM, we generated a perfectly rectangular 400×200 cm slab, with supports on both the short sides and on one meter of one of the long sides.
Scheme of the model in Dlubal RFEM
Applying a 3kN/m2 uniform load, we analysed the variation of support reactions and displacements in the events of:
-
Homogeneous wooden panel (class C24, thickness 200 mm)
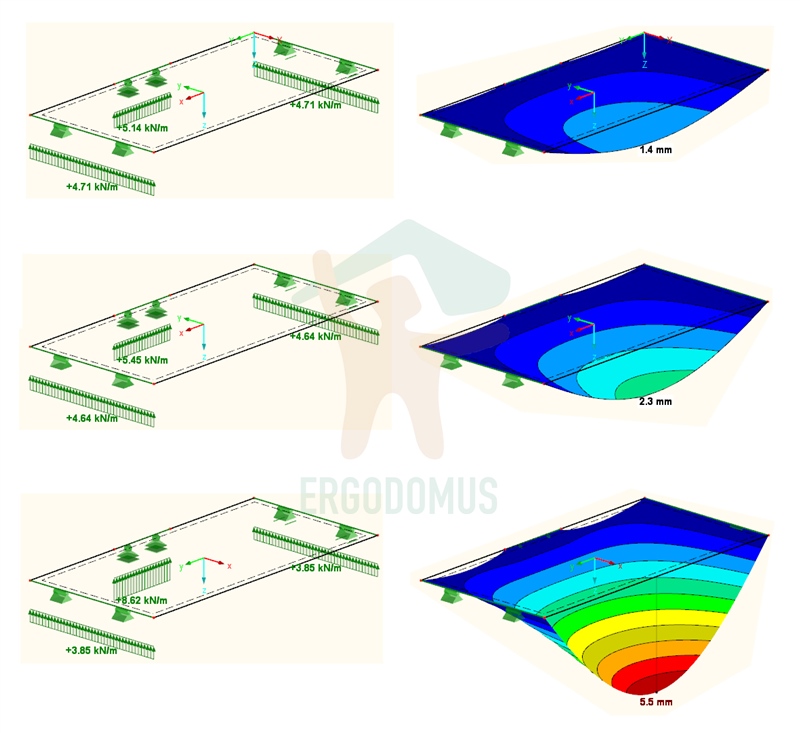
The panel has been modelled as a ‘surface’ element, to whom the 200mm thickness and the C24 orthotropic mechanical features were assigned. The main direction must be parallel to the long sides (y-axis of the global reference), and consequentially the surface’s orientation was correctly rotated 90 degrees from the global reference (as demonstrated by the position of the local x-axis in the centre of the surface).
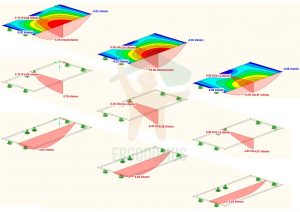
As expected, the maximum displacement takes place in the middle of the non-supported long side of the slab.
Geometric and mechanical properties of the homogeneous panel
Support reactions (averaged on the length)
Displacements
-
5-layers Xlam panel (every layer 40mm thick, for a total of 200mm), with correct main direction
Even the Xlam panel was modelled as a ‘surface’ element, to whom a separately-evaluated stiffness matrix was assigned, containing both geometric data (regarding number and thickness of layers) and mechanical characteristics (for more information about the definition of the matrix, see ‘Xlam: Evaluation of the correct stiffness matrix’). In this case, we modelled a 5-layers panel composed of wooden boards (class C24, thickness 40mm and 0-90-0-90-0 orientation).
Geometric and mechanical properties of the Xlam panel
Having only three layers parallel to the local x-axis, in this direction the slab is less stiff than case 1. In fact, a slight decrease in support reactions corresponds to a marked increase in displacements (of more than 60%, compared to the homogeneous panel – 2,3 vs 1,4 mm).
On the contrary, having two layers in the same direction as the local y-axis, in that direction the slab is slightly more stiff than the previous one, as proved by the faint increase in support reactions (5,45 vs 5,14 kN/m).
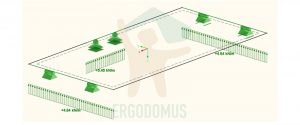
Support reactions (averaged on the length)
Displacements
-
5-layers Xlam panel (every layer 40mm thick, for a total of 200mm), with incorrect main direction
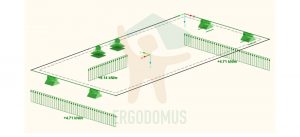
This last example shows the serious consequences of laying a Xlam slab with the main layers perpendicular to the slab’s planned direction. The previous case’s slab was rotated 90 degrees, to have this orientation: 90-0-90-0-90.
Example of mistaking the main direction of the slab
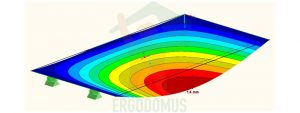
As you can see from the following pictures, a slab like this is very unlikely to be verified because, having only two resistant layers in the direction of the long side, displacements in the middle will be much greater than in case 1. or 2. (5,5 vs 2,3 vs 1,4).
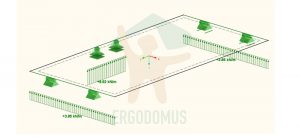
Support reactions (averaged on the length)
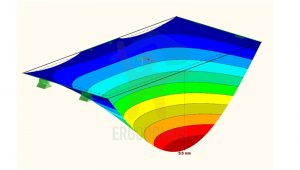
Displacements
Based on the results discussed so far, the following considerations may be made:
- The correct way of modelling a Xlam panel is certainly the one shown in example n.2.
- The mechanical response of a Xlam panel cannot be compared to the one of a homogeneous massive wooden panel. For this reason, during modelling it is impossible to make such a simplification without making important mistakes in the evaluation of support reactions, displacements and dynamic behaviour. Being the orthotropy of Xlam not only due to the intrinsic characteristics of wood but also to its structure (composed of crossed and perpendicular layers), it is necessary to define a correct stiffness matrix before modelling.
- Designed orientation of panels must always be respected, both when ordering and laying the material, in order to avoid dangerous stresses and displacements, as seen in the last example.
|
Type of panel |
Support reaction in x (kN/m) |
Support reaction in y (kN/m) |
Displacements (mm) |
| Homogeneous |
4.71 |
5.14 |
1.4 |
| Xlam |
4.64 |
5.45 |
2.3 |
| Rotated Xlam | 3.85 | 8.62 |
5.5 |